A mathematician has just solved a $ 1 million problem, aged 160

A renowned mathematician claimed to have developed a proof of the Riemann Hypothesis, a 160-year-old mathematical problem with a $ 1 million bonus.

Michael Atiyah, a mathematician who has won several of the highest awards in mathematics, gave a lecture at the Heidelberg Winners' Forum in Germany on Monday to explain his demonstration of Riemann's hypothesis, which had been formulated by Bernhard Riemann in 1859 when it is used as an argument for a given function – but it gave up trying to provide proof.

As Atiyah pointed out during his intervention, Riemann's hypothesis "has been verified numerically for millions and millions with every computer we can think of, but there is no evidence ". to explain the strange distribution of prime numbers among other mathematical quirks.

If Atiyah's proof is correct, it would be a large Deal for the Mathematics Community – Providing evidence of Riemann's hypothesis over the last 160 years has become one of the most thorny problems in mathematics. Since 2000, Clay Mathematics Institute has offered a million dollar award to the mathematician who publishes his findings in a peer-reviewed journal and waits two years for other mathematicians to formulate any objections to the solution. . Although Atiyah demonstrated his evidence on Monday, its publication has not yet been accepted in a peer-reviewed journal.

"Riemann's hypothesis has been proven, unless you are the type of person who does not believe the evidence by contradiction," Atiyah said at his Heidelberg conference. "In that case, I have to go back and think again. But people generally accept the proof by contradiction, so I would say that I deserve the prize. "

Read more: Researchers discover a model for the seemingly random distribution of prime numbers

But many mathematicians have expressed reservations about the legitimacy of the solution, since Atiyah had already claimed to provide evidence of major mathematical problems before its solutions were examined or published.

If the proof of Atiyah does not hold, it would not be the first time that a mathematician claims to have cracked for Riemann. In 2015, an unknown Nigerian professor named Opeyemi Enoch claimed to have provided evidence of Riemann's hypothesis, but everything turned out to be a sham. Unlike Enoch, Atiyah won both the Fields Medal and the Abel Award, which are essentially Nobels for mathematicians.

As Markus Pössel, a German astronomer at the Atiyah conference, said, it is too early to determine whether the evidence is legitimate.

"The specialists in this field do not yet have sufficient information to properly judge this claim," said Pössel. "In particular, Atiyah used an unusual function he called the" Todd function "after one of his teachers. I do not know if this function really exists in the form claimed by Atiyah. It is certainly reasonable to be cautious about this. "

WHAT IS THE HYPOTHESE OF RIEMANN?

In 1859, the mathematician Bernhard Riemann hypothesized the moment when a particular function returns a value of zero. The hypothesis has a number of practical applications in mathematics, especially as an explanation of the strange distribution of prime numbers, which are only divisible by themselves and by one.

Riemann's hypothesis concerns the values ​​used in the zeta function, which produce a series of convergent or divergent numbers depending on the value of s– known as the function argument – in the following order:

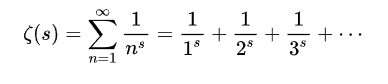
Zeta function of Riemann. Image: Wikimedia Commons

Riemann's insight was that the zeta function could also be extended to complex numbers, which are a combination of imaginary and real numbers. (Quick Recall: Real numbers are those that can be considered as points on a line, while imaginary numbers such as -1, represented by I, can not. So, for example, 3 + 5 I is a complex number.)

As Edward Frenkel explains in a video for Numberphile, if you plug a real number into the zeta function, for example "2", you get the series "1+ ¼ + 1/9 + 1/16 …". which are discovered in this sequence and added up, plus they get closer to a certain total known as the limit. If the series approaches a limit, then it is considered a convergent series.

On the other hand, if a number like "-1" is used as argument for the zeta function, it returns a series "1 + 2 + 3 + 4 + 5 …". This type of series has no limit since the sum of the number continues to grow and is known as the divergent series.

Riemann argued that if a complex number is used as an argument for the zeta function, the result is a convergent series. When certain numbers are used as the real number input for a zeta function whose argument is a complex number, it returns a value of zero.

Some of these inputs are trivially easy to discover. For example, -2, -4, and -6 will return all zero. But Riemann's hypothesis was that if ½ were used as a real number for the complex argument of a zeta function, any imaginary number with which it would be associated would also return zero. So ½ + 1 I, ½ + 2 I, ½ + 3 I, and so on would all come back to zero.

"For which values ​​is the zeta function equal to zero?" Said Frenkel in the Numberphile video. "That's the million dollar question."

Atiyah's evidence claims to answer this question by relying on something he calls the "Todd function," named after the late mathematician and former Atiyah professor, J.A. Todd. As pointed out by Pössel, the novelty of this function is at the origin of the skepticism of many mathematicians with regard to the proofs of Atiyah.

If Atiyah hopes to claim the million dollar award for breaking the millennium problem, the name given to the seven most difficult mathematical problems according to the Clay Mathematics Institute, then the Todd function will have to withstand rigorous scrutiny by D & D. Other mathematicians over the next two years.

So far, only one of the seven millennial problems has been solved, even though dozens of solutions to various problems have been proposed. This reflects the difficulty of the problems to be solved and the importance of peer review in mathematics. Even if Atiyah's proofs ultimately miss the mark, his solution will certainly be at the forefront of some of the brightest mathematicians in the world for the next few years.