
[ad_1]
<! –
->

The position of Comet Halley in May 2019. The view is on the north side of the solar system. Although the planets revolve around our sun counterclockwise, the Halley comet rotates clockwise. Click here for the current position of Comet Halley or to change the date to display its position for any chosen year.
Halley's Comet, proud parent of two meteor showers, switches to the inner solar system every 76 years or so. At this point, the heat of the sun causes the comet to loosen its icy grip on its agglomeration of ice, dust and gas the size of a mountain. At each passing near the sun, the friable comet throws a new trail of debris into its orbital flow. It lost about 1 / 1000th of its mass during its last flyby in 1986. This is because comets like Halley are so friable that we see annual meteor showers, like the Eta Aquariid meteor shower that is currently taking place .
Read on to learn more about Comet Halley, the meteor showers it causes, and how astronomers calculate the speeds of meteors in our sky.

Comet Halley May 29, 1910 via Wikimedia Commons.

The Kuiper Aerial Observatory acquired this image of Comet Halley in April 1986, the comet crossing in front of the Milky Way. Image via NASA.
The two meteor clouds of the comet Halley. Because the Halley comet has circled the sun countless times over countless millennia, cometary fragments punctuate its orbit. That's why the comet does not have to be near the Earth or the sun to produce a meteor shower. Instead, each time our Earth in orbit intersects with Halley's comet, fragments of comets – often no larger than grains of sand or granules of gravel – crush in the upper atmosphere of the planet. Earth to vaporize in the form of fiery trails in the sky: the meteors.
It turns out that we do not cross the orbit of Comet Halley not once, but twice a year. In early May, we see fragments of this comet as the annual meteor shower Eta Aquariid.
About six months later, in October, the Earth in orbit crosses the orbital path of comet Halley again. This time, these fragmented fragments of Halley's Comet burn in the Earth's atmosphere under the annual Orionid meteor shower.
By the way, these little fragments are called meteorites when in space, and meteors when they vaporize in the Earth's atmosphere.
Meteors in annual showers – made from frozen debris from comets – do not touch the ground. They vaporize very high in the Earth's atmosphere. The more rocky or metallic meteors are sometimes what strikes the ground intact, and then they call each other meteorites.
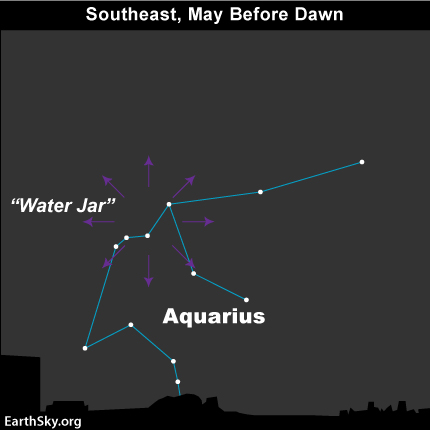
Eta Aquariid meteors seem to emit near a famous asterism – or a notable star pattern – called the water pot in Aquarius. The shower arrives on the morning of May 4th, 5th and 6th, 2019.
Where is Comet Halley now? Astronomers often like to indicate the distances of solar system objects in terms of astronomical units (AU), which is the sun-earth distance. Comet Halley is 0.587 AU from the sun at its nearest point of the sun (perihelion) and 35.3 AU at its furthest point (aphelion).
In other words, Halley's comet is about 60 times farther away from the sun than its farthest away.
It was at perihelion for the last time in 1986 and will be back to perihelion in 2061.
At present, Halley's comet is outside Neptune's orbit and not far from its aphelion. See the image at the top of this article – for May 2019 – via Fourmilab.
Even though the meteroids swim in the orbit of Halley's comet, each time the Earth crosses Halley's comet's orbit in May and October, these meteorites turn into glowing meteors once they plunge into the high atmosphere of the Earth.

The side view shows that the orbit of Halley's comet is very sloping with respect to the plane of the ecliptic. The green color represents the part of the orbit located south of the ecliptic (Earth-Sun orbital plane), while the blue highlights the part of the orbit located north of the 39; ecliptic.
Of course, Comet Halley is not the only one to produce a major meteor shower …
Parent bodies of other large meteor showers
| Meteor shower | Parent body | Half-major axis | Orbital period | perihelion | Aphelion |
| Quadrantid | 2003 EH1 (asteroid) | 3.12 AU | 5.52 years | 1.19 AU | 5.06 AU |
| The lyrids | Comet Thatcher | AU $ 55.68 | 415 years | 0.92 AU | 110 AU |
| Eta Aquariids | Comet 1 / P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| Aquariids Delta | Comet 96P / Machholz | 3.03 AU | 5.28 years | 0.12 AU | AU 5.94 |
| Perseids | Comet 109P / Swift-Tuttle | 26.09 AU | 133 years | 0.96 AU | 51.23 AU |
| Draconides | Comet 21P / Giacobini – Zinner | 3.52 AU | 6.62 years | 1.04 AU | 6.01 AU |
| Orionids | Comet 1 / P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| taurides | Comet 2P / Encke | 2.22 AU | 3.30 years | 0.33 AU | 4.11 AU |
| Leonids | Comet 55P / Tempel-Tuttle | 10.33 AU | 33.22 years | 0.98 AU | AU $ 19.69 |
| Geminids | 3200 Phaethon (asteroid) | 1.27 AU | 1.43 years | 0.14 AU | AU 2,40 |
How fast do comet Halley's meteors move? If we can determine how fast Halley comet moves at the Earth's distance from the Earth, we should also be able to determine how fast these meteors fly in our sky.
Some of you may know that a solar system body, such as a planet or comet, goes faster in its orbit when it approaches the sun. and more slowly in its orbit as it moves away. Halley's comet rocks in the orbit of Venus at perihelion – the closest point of the comet to the sun. AT aphelion – its furthest point – Halley's comet goes well beyond the orbit of Neptune, the outermost (known) planet of the solar system.

In this diagram, we look at the north side of the solar system plane. The planets revolve around the sun counterclockwise and Halley's comet turns around the sun in a clockwise direction.
When the meteoroids of the orbital current of Halley's Comet cross the sky as Eta Aquariid or Orionid meteors, we know that these meteoroids / meteors must be an astronomical unit (distance from the Earth) from the sun. It might be tempting to assume that these meteoroids of an astronomical unit of the Sun travel in space at the same speed as the Earth: 108,000 km / h.
However, the velocity of these meteoroids across space is not equal to that of the Earth at the distance from the Earth to the sun. For this to happen, Earth and Halley's Comet should spin around the sun in the same amount of time. But the orbital periods of Earth and Comet Halley are very different. The Earth takes a year to turn around the sun while Halley's comet takes about 76 years
However, thanks to the great genius Isaac Newton, we can calculate the velocity of these meteoroids / meteors at the distance from the Earth to the sun using Newton's Vis-viva equation, his poetic interpretation of instantaneous motion.
The answer, giving the speed of these meteoroids through the space at the distance of the Earth from the sun, is practically at hand. All we need to know is the semi-major axis of the comet Halley (average distance from the sun) in astronomical units. Here you have it:
The half-major axis of the comet Halley = 17.8 astronomical units.
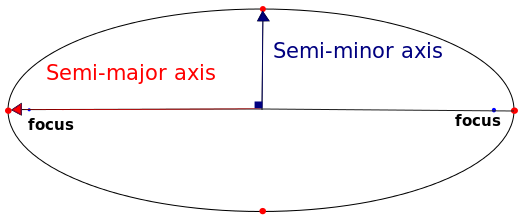
Once we know the major half-axis of a comet in astronomical units, we can calculate its velocity at any distance from the sun with Vis-viva's easy-to-use equation. The sun resides on one of the two foci of the elliptical orbit of the comet.
In the easy-to-use Vis-viva equation below, r = distance of the sun in astronomical units and a = half-major axis of the comet Halley's orbit in astronomical units. In other words, r = 1 AU and a = 17.8 AU.
Vis-viva equation (r = distance from the sun = 1 AU, and a = half-major axis = 17.8 AU):
Speed = 67,000 x the square root of (2 / r – 1 / a)
Speed = 67,000 x the square root of (2/1 – 1 / 17.8)
Speed = 67,000 x the square root of (2 – 0,056)
Speed = 67,000 x the square root of 1,944
Speed = 67,000 x 1.39
Speed = 93,130 miles per hour or 25.87 miles per second
The answer above gives the speed of these meteoroids through the space at the distance from the Earth of the sun. However, if these meteoroids hit the Earth's atmosphere hard, the speed would increase to 257,704 km / h (160,130 miles per hour), as 93,130 + 67,000 = 160,130. NASA gives the speed of meteors Eta Aquariid and Orionid at 238,000 km / h (148,000 miles per hour), suggesting that the collision of these meteoroids / meteors with the Earth is not so far away.
We can also use the Vis-Viva equation to determine the velocity of Halley's comet (or its meteoroids) at the distance between perihelion of 0.59 AU and aphelion distance of 35.3 AU.
Perihelion velocity = 122,331 miles at the hour (200,000 km / h)
Speed Aphelion = 1,464 miles per hour (2,400 km / h)
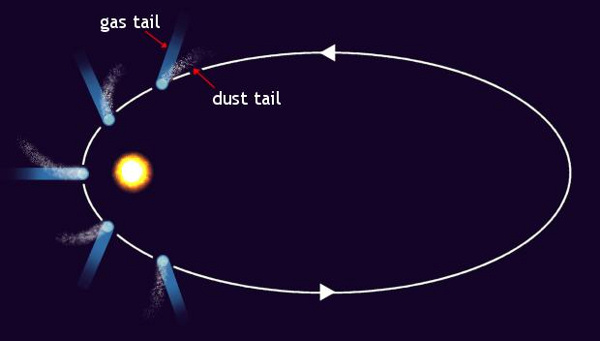
Comets develop tails of gas and dust as the sun approaches. Depending on the comet, it can orbit the sun counter-clockwise (as above) or clockwise (as Halley does). Read more: Why do comets develop tails?
In summary: the famous comet Halley is at the origin of Eta Aquariids (which are currently taking place) and Orionids in October. And also where the comet, the parents' body of other meteor showers … and Isaac Newton's Vis-Viva equation, his poetic interpretation of instantaneous movement.

[ad_2]
Source link