Curious Observer’s Guide to Quantum Mechanics, pt. 4: Looking at the stars

by



[ad_1]

Curious Observer's Guide to Quantum Mechanics, pt. 4: Looking at the stars

Aurich Lawson / Getty Images

One of the quietest revolutions of our present century has been the entry of quantum mechanics into our everyday technology. In the past, quantum effects were confined to physics labs and delicate experiments. But modern technology increasingly relies on quantum mechanics for its basic operation, and the importance of quantum effects will only increase in the decades to come. As such, physicist Miguel F. Morales has taken on the Herculean task of explaining quantum mechanics to the rest of us laymen in this seven-part series (no math, we promise). Below is the fourth story in the series, but you can still find the starting story as well as a landing page for the entire series so far on the site.

Beautiful telescoping images of our Universe are often associated with the majestic and classical physics of Newton. While quantum mechanics dominates the microscopic world of atoms and quarks, the movements of planets and galaxies follow the majestic clockwork movement of classical physics.

But there is no natural limit to the size of quantum effects. If we look closely at the images produced by telescopes, we see the fingerprints of quantum mechanics. This is because the particles of light have to travel across the vast expanses of space like a wave to create the beautiful images we enjoy.

This week, we’ll focus on how photons travel across light years and how their inherent quantum ripple enables modern telescopes, including Earth-sized interferometric telescopes.

Stars light

How to think of the light of a distant star? Last week, we used the analogy of a pebble falling into a lake, with the ring of ripples on the water replacing the wave motion of photons. This analogy has helped us understand the length of a particle ripple and how photons overlap and cluster.

We can continue this analogy. Each star similar to the Sun, in that it makes a lot of photons. As opposed to someone carefully dropping simple pebbles into a mirror-smooth lake, it’s more like they’ve poured into a bucket of gravel. Each pebble makes a ring of ripples, and the ripples of each stone spread out as before. But now the ripples are constantly mixing and overlapping. As we watch the waves ride the distant shore of Earth, we don’t see the ripples of each individual pebble; instead, the combination of many individual waves has been added.

The chaotic waves of a gravel star crossing our pond. The ripples of many pebbles overlap, creating a complex set of waves.
Enlarge / The chaotic waves of a gravel star crossing our pond. The ripples of many pebbles overlap, creating a complex set of waves.

Miguel Morales placeholder image

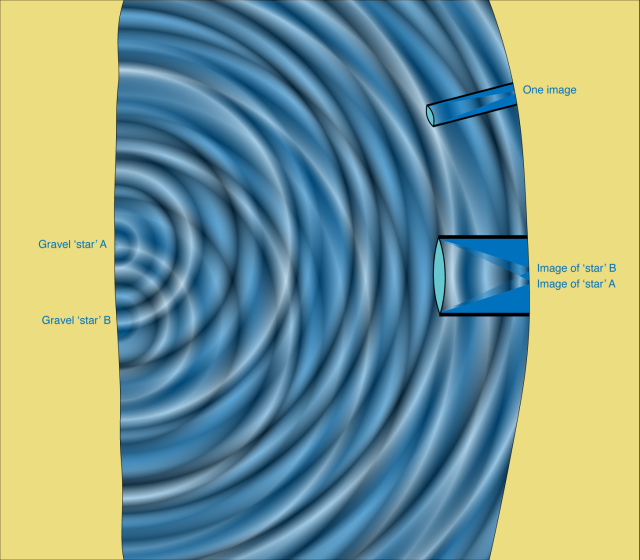
So let’s imagine we are standing on the shore of a lake as the waves roll in, looking at our gravel “ star ” with a telescope for the water waves. The telescope’s lens focuses the star’s waves on a point: the place on the camera’s sensor where that star’s light lands.

If a second bucket of gravel falls into the lake further along the opposite shore, the ripples will overlap at our shore, but will be focused by the telescope at two separate points on the detector. Likewise, a telescope can sort starlight into two distinct groups: photons from star A and photons from star B.

But what if the stars are very close to each other? Most of the “stars” that we see at night are in fact double stars – two suns so close together that they appear as a single shining point of light. When in distant galaxies, stars can be separated by light years while still looking like a single point in professional telescopes. We would need a telescope that could sort of sort through the photons produced by different stars to resolve them. Similar things apply if we want to image features like sunspots or flares on the surface of a star.

Coming back to the lake, there is nothing special about the ripples made by different pebbles – the ripples of one pebble are indistinguishable from the ripples made by another. Our wave telescope doesn’t care if the ripples are from different pebbles in a bucket or from different buckets in total – a ripple is a ripple. The question is how far apart two pebbles must be dropped so that our telescope can distinguish that the ripples came from different places.

Sometimes when you are stumped it is best to take a slow walk along the beach. So we’re going to have two friends sit on the far shore dropping pebbles, while we walk along our shore, watching the waves and thinking deeply. As we walk along the beach, we see that our friends’ waves are overlapping everywhere, and the waves are coming at random. There doesn’t seem to be any pattern.

  • The waves of two “stars” of gravel. Each star’s waves are circular (see subsequent panels), but combine into an apparent clutter. However, we notice that while the wave train at each location is chaotic, at places close to each other on the beach, the wave trains are very similar. In places far from the beach we see a completely different wave train.

    Miguel Morales placeholder image

  • The waves of a single star.

    Miguel Morales placeholder image

  • The waves of the other star. The waves can be combined to produce the wave pattern seen in the first panel.

    Miguel Morales placeholder image

But on closer inspection, we notice that spots on the beach very close to each other see almost identical waves. Waves are random in time, but places on the beach within walking distance of each other see the even random train of waves. But if we look at the waves hitting far away on the beach, this wave train is completely different from the one hitting near us. Two places close to the beach will see almost identical wave trains, but widely separated places on the beach will see different wave trains.

It makes sense if we think of the waves on the beach as the combination of tiny ripples of hundreds of pebbles. At nearby places on the beach, the undulations of the pebbles released by the two friends add up in the same way. But further along the beach a friend’s ripples will have to travel further, so the ripples add up in a different way, giving us a new set of waves.

While we can no longer see the ripples of the individual pebbles once they combine into waves, we can measure the distance it takes to see a new wave train. And that tells us something about how the ripples add up.

We can confirm this by asking our two stony friends to come closer. When our friends are close to each other, we notice that we have to walk a long way along our beach to see the ripples add up in a different way. But when our friends are far away, a few steps on our beach will make the wave trains look different. By varying the distance to travel before the waves look different, we can determine how far away our friends falling from the rocks are.

Large and small telescopes looking at the same two stars. Because the waves look different at the far edges of the large telescope, it can sort the waves into two sources. For the small telescope, the waves look the same through the lens, so it sees both stars as one unresolved source.
Enlarge / Large and small telescopes looking at the same two stars. Because the waves look different at the far edges of the large telescope, it can sort the waves into two sources. For the small telescope, the waves look the same through the lens, so it sees both stars as one unresolved source.

Miguel Morales placeholder image

The same effect occurs with photonic waves, which can help us understand the resolution of a telescope. Looking at a distant binary star, if the light waves entering the opposite edges of the telescope look different, then the telescope can sort the photons into two distinct groups – the photons from star A and photons from star B. But if the light waves entering the opposite edges of the telescope look the same, then the telescope can no longer sort the photons into two groups and the binary star will look like a single point on our telescope.

If you want to solve close objects, the obvious thing to do is to enlarge the diameter of the telescope. The further away the edges of the telescope are, the more stars can and still be distinguished. Larger telescopes have better resolution than smaller telescopes and can separate light from sources closer together. This is one of the big ideas behind building really huge telescopes that are 30 or even 100 meters in diameter – the bigger the telescope, the better the resolution. (This is still true in space, and true in the field with adaptive optics to correct atmospheric distortions.)

For telescopes, it’s really better.

[ad_2]

Source link