[ad_1]
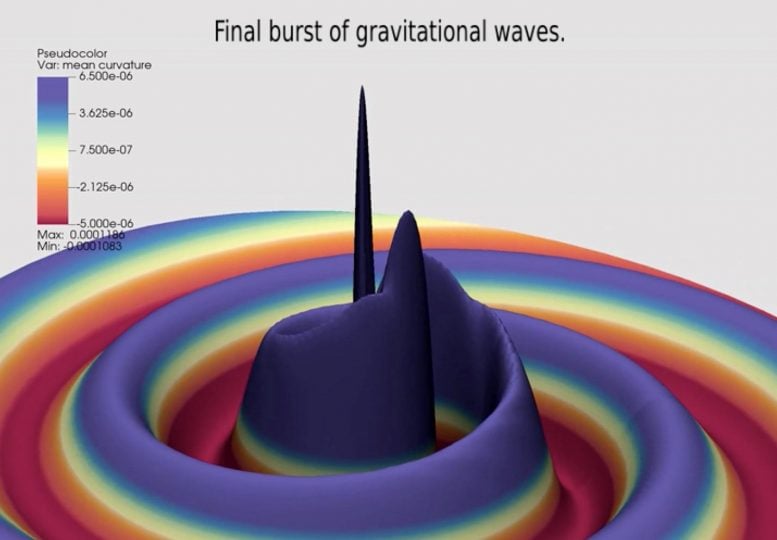
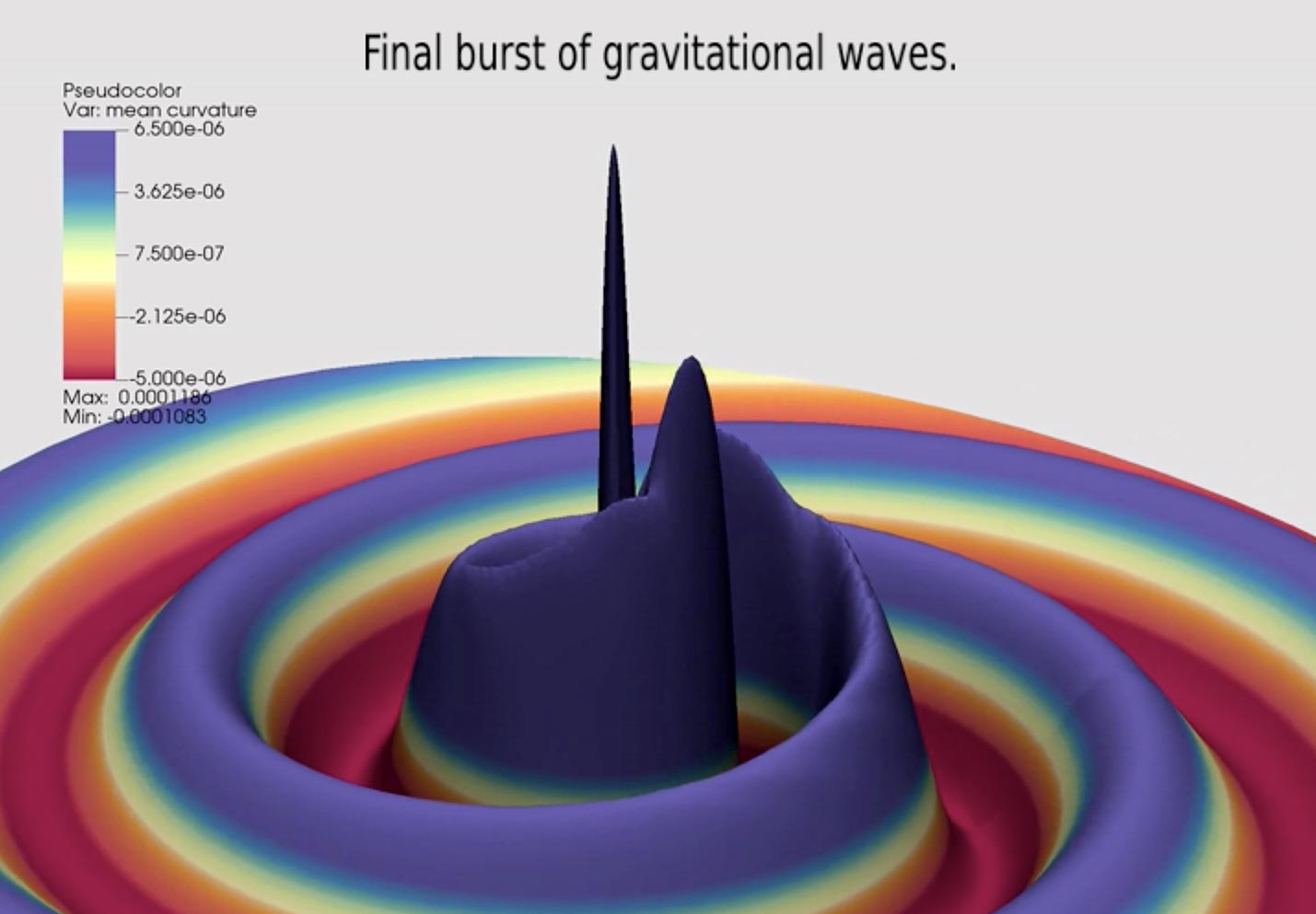
Image taken from an animation of the inspiration of a binary black hole with a mass ratio of 128: 1 showing the beginning of the last burst of gravitational waves. Credit: Carlos Lousto, James Healy, RIT
Final dance of the unequal partners of the black hole
Rochester Institute of Technology Scientists Perform First-Ever Large Mass Report Simulation black hole merger on Frontera.
Solving general relativity equations for black hole collisions is not easy.
Physicists began using supercomputers to find solutions to this famous problem in the 1960s. In 2000, with no solutions in sight, Kip Thorne, 2018 Nobel laureate and one of the designers of LIGO, famous bet that there would be an observation of gravitational waves before a digital solution is found.
He lost that bet when, in 2005, Carlos Lousto, then at the University of Texas at Brownsville, and his team generated a solution using the Lonestar supercomputer at the Texas Advanced Computing Center. (At the same time, groups at NASA and independent solutions derived from Caltech.)
In 2015, when the Laser Interferometer Gravitational-Wave Observatory (LIGO) first observed such waves, Lousto was in shock.
“It took us two weeks to realize that it was really nature and not entering our simulation as a test,” said Lousto, now professor of mathematics at the Rochester Institute of Technology (RIT). “The comparison with our simulations was so obvious. You could see with your bare eyes that it was the fusion of two black holes.
Lousto is back with a new milestone in numerical relativity, this time simulating the fusion of black holes where the mass ratio of the largest black hole to the smallest is 128: 1 – a scientific problem bordering on what is possible calculation. Its secret weapon: TACC’s Frontera supercomputer, the eighth most powerful supercomputer in the world and the fastest of all universities.
His research with collaborator James Healy, supported by the National Science Foundation (NSF), has been published in Physical examination letters this week. It may take decades to confirm the results experimentally, but it nonetheless serves as a computational achievement that will help advance the field of astrophysics.
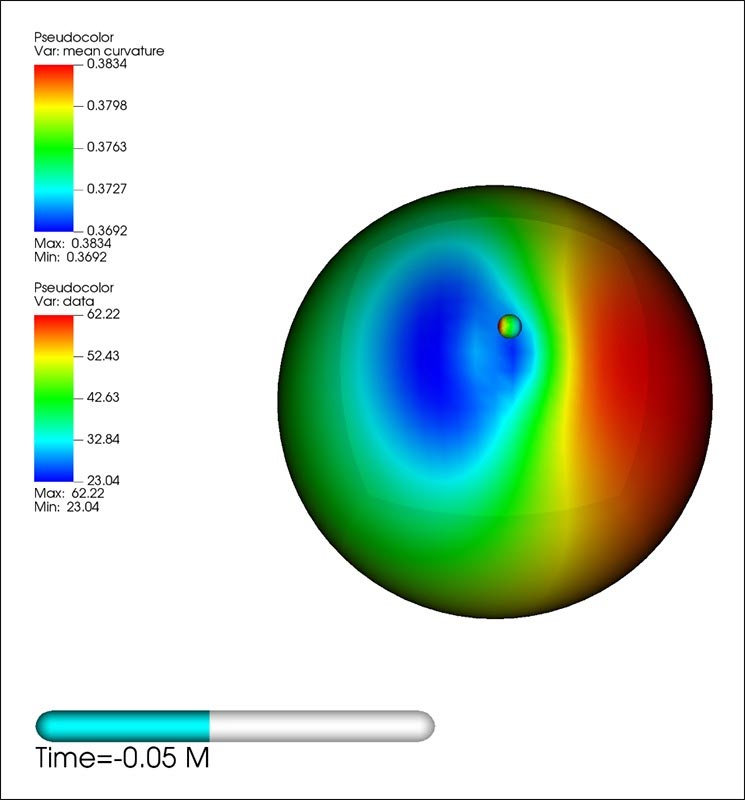
Color map of the curvature on the horizon of the large black hole generated by the small black hole near fusion. Credit: Nicole Rosato
“Modeling pairs of black holes with very different masses is very computationally demanding due to the need to maintain precision in a wide range of grid resolutions, ”said Pedro Marronetti, director of the gravitational physics program at NSF. “The RIT Group has performed the world’s most advanced simulations in this area, and each one brings us closer to understanding the observations that gravitational wave detectors will provide in the near future.”
LIGO can only detect gravitational waves caused by small and medium-mass black holes of roughly equal size. It will take observatories 100 times more sensitive to detect the type of mergers that Lousto and Healy have modeled. Their results show not only what gravitational waves caused by a 128: 1 fusion would look like to an observer on Earth, but also the characteristics of the ultimate fused black hole, including its final mass, rotation and recoil speed. This led to some surprises.
“These fused black holes can have speeds much greater than what was previously known,” Lousto said. “They can travel 5,000 kilometers per second. They come out of a galaxy and roam the universe. This is another interesting prediction.
The researchers also calculated the gravitational waveforms – the signal that would be perceived near Earth – for such mergers, including their peak frequency, amplitude, and brightness. By comparing these values with the predictions of existing scientific models, their simulations were less than 2% of expected results.
Previously, the largest mass ratio ever solved with high precision was 16 to 1, eight times less extreme than Lousto’s simulation. The challenge of simulating larger mass ratios is that it requires solving the dynamics of interacting systems at additional scales.
Like computer models in many fields, Lousto uses a method called adaptive mesh refinement to obtain precise models of the dynamics of interacting black holes. This involves placing the black holes, the space between them, and the distant observer (us) on a grid or mesh, and refining areas of the mesh in more detail where needed.
Lousto’s team approached the problem with a methodology that he compares to Zeno’s first paradox. By halving and halving the mass ratio while adding internal levels of grid refinement, they were able to go from black hole mass ratios of 32: 1 to bit systems of 128: 1 that undergo 13 orbits before fusion. On Frontera, it took seven months of constant computation.
“Frontera was the perfect tool for the job,” Lousto said. “Our problem requires high performance processors, communication, and memory, and Frontera has all three.”
Simulation is not the end of the road. Black holes can have a variety of spins and patterns, which affect the amplitude and frequency of gravitational waves that their fusion produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “models” to compare with future detections.
The results will help designers of future terrestrial and space gravitational wave detectors plan their instruments. These include advanced third-generation ground-based gravitational wave detectors and the Laser Interferometer Space Antenna (LISA), which is slated for launch in the mid-2030s.
Research can also help answer fundamental mysteries about black holes, such as how some can get so large – millions of times the mass of the Sun.
“Supercomputers help us answer these questions,” Lousto said. “And the issues inspire new research and pass the torch to the next generation of students.”
Reference: “Exploring the Small Mass Ratio Binary Black Hole Merger via Zeno’s Dichotomy Approach” by Carlos O. Lousto and James Healy, November 5, 2020, Physical examination letters.
DOI: 10.1103 / PhysRevLett.125.191102
[ad_2]
Source link