Curious Observer’s Guide to Quantum Mechanics, pt. 3: pink color glasses

So far, we’ve seen particles move like waves and learned that a single particle can take multiple, widely separated paths. There are a number of questions that naturally arise from this behavior, one of them being, “How big is a particle?” The answer is remarkably subtle, and over the next couple of weeks (and articles) we’ll be exploring different aspects of this question.

Today we will start with a seemingly simple question: “How long is a particle? “

Go long

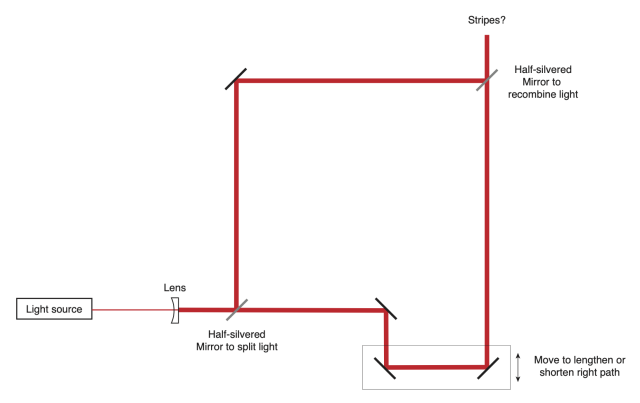
To answer this, we have to think of a new experience. Previously, we sent a photon on two very different paths. While the paths were widely separated in this experiment, their lengths were the same: each went around both sides of a rectangle. We can improve this setup by adding a few mirrors, which allows us to gradually change the length of one of the paths.

When the paths are the same length we see stripes like we did in the first article. But as we lengthen or shorten one of the paths, the stripes slowly fade. This is the first time that we have seen stripes slowly disappear; in our previous examples, the stripes were there or not.

We can tentatively associate this fading of the stripes when we change the path length with the length of the photon traveling on the way. The stripes only appear if the waves of a photon overlap when they are recombined.

But if the particles travel in the form of waves, what do we even mean by length? A useful mental image may be to drop a pebble into a pool of fresh water. The resulting ripples propagate in all directions in the form of a set of rings. If you draw a line from where the rock fell through the rings, you will find that there are five to 10. In other words, there is thickness to the ring of waves.

Another way of looking at it is as if we are a cork on the water; we would not feel any waves, a period of waves, then soft water again after the ripple passed. We would say the “ length ” of the ripple is the distance / time we have experienced waves.

Likewise, we can think of a traveling photon as a set of ripples, a block of waves entering our experience. The waves divide naturally and travel both paths, but they can only recombine if the two path lengths are close enough for the ripples to interact when they come together. If the paths are too different, one set of undulations will have already exceeded before the other arrives.

This image is a good explanation of why the stripes fade slowly: They are strong when there is a perfect overlap, but fade as the overlap decreases. By measuring how far the stripes disappear, we measured the length of the ripples in the particle.

Rummage in the bulb drawer

We can go through our usual experiments and see the same characteristics that we have seen before: lowering the photon rate (which produces paintball pointillism of stripes), changing the color (bluer colors mean tighter spacing), etc. But now we can also measure the behavior of the bands when we adjust the path length.

While we often use lasers to generate light particles (they are great photonic dot shooters), any type of light will do: an incandescent bulb, an LED light, a neon light, sodium street lamps, a star light, a light passed through colored filters. No matter what type of light we are sending, create stripes when path lengths match. But the stripes fade at distances ranging from microns for white light to hundreds of kilometers for the highest quality lasers.

Light sources with distinct colors tend to have the longest ripples. We can study the color properties of our light sources by sending their light through a prism. Some of the light sources have a very narrow color gamut (laser light, neon light, sodium street light); some have a large rainbow of colors (the incandescent bulb, the LED mood light, the starlight); while others, such as sunlight sent through a color filter, are intermediate in the range of composite colors.

What we do notice is that there is a correlation: the narrower the color gamut of the light source, the longer the path difference can be before the stripes disappear. The color itself doesn’t matter. If I choose a red filter and a blue filter that pass the same width of colors, their stripes will disappear at the same path difference. It’s the interval the color that matters, not the average color.

Which brings us to a rather surprising result: the length of a particle wave is given by the range of colors (and therefore of energies) at its disposal. Length is not a defined value for a particular type of particle. By simply rummaging through our drawer of light sources, we produced photons of lengths ranging from microns (white light) to a few cm (a laser pointer).