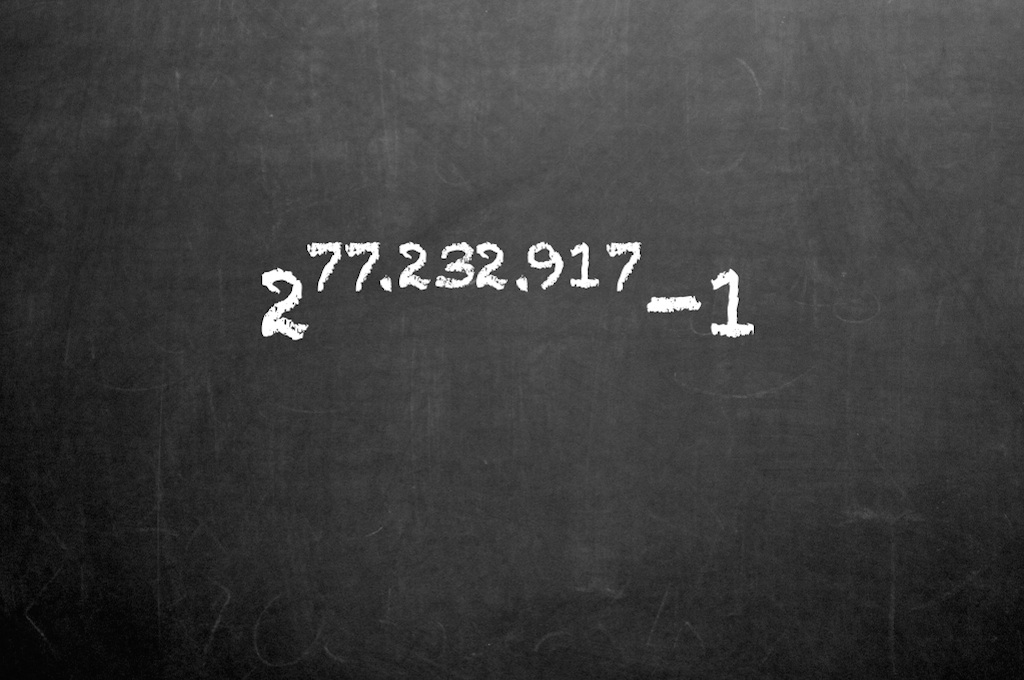
[ad_1]
(td) nirak / Flickr
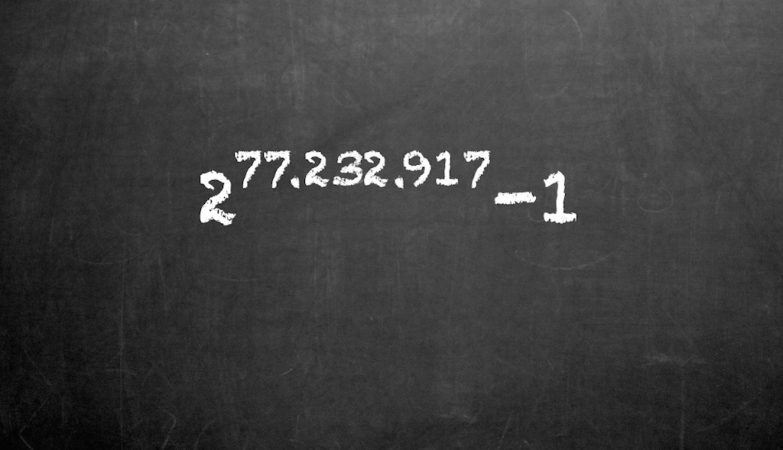
Mathematicians, Professionals and Fans in a Global Research Project – The Great Internet Mersenne Prime Search (GIMPS) – Discovered the Biggest Cousin Known To Date . Mersenne Prime Search (GIMPS) discovered the highest prime number known to date: abbreviated as 2 82,589,933 -1, the number contains 24,862,048 more than 39; one and a half million digits higher than the previous record prime number discovered in 2017.
This number belongs to a special clbad of rare prime numbers, called Mersenne cousins, and is only the [51459008] the 51st cousin of Mersenne already discovered
According to Sci-News, the newly discovered prime number was baptized M82589933 and was discovered when calculating two out of 82,589,933, subtracting a .
A cousin of Mersenne is a prime number of form 2 P -1. As numbers grow, prime numbers – a number divisible by 1 and by itself – become more and more difficult to find .
As they become more and more distant and distant there is no distribution model, it is not possible to use an algorithm to know these numbers.
The first cousins of Mersenne are 3, 7, 31 and 127, which corresponds to P = 2, 3, 4, 5, 6, 5 and 7, respectively. Mersenne's cousins have been at the heart of number theory since they were first discussed by the Greek mathematician Euclid around 350 BC. J.-C.
The man whose name has its origin, the French monk Marin Mersenne (1588-1648), made a famous conjecture on which the values of P would give a cousin.
In this way, Euclid proved that each Mersenne cousin generates a perfect number – a number whose proper divisors add up to the number itself. For example, the smallest perfect number is 6 = 1 + 2 + 3 and the second perfect number is 28 = 1 + 2 + 4 + 7 + 14.
Swiss mathematician Leonhard Euler (1707-1783), at their turn, all the perfect numbers come from Mersenne's cousins. The newly discovered perfect number is 2 82 589 932 * (2 82 589 933 -1) A number that has more than 49 million digits.
Source link